|
Pedagogica describes a number of teaching/learning situations in the grade school through university curriculum where careless use of language confuses students. It is a plea to:
Teach it right the first time.
Q. Why include a page on teaching Mathematics on a philology and humour site?
A1. Because I feel like it; it's my site, and I can do what I please.
A2. Because comprehending Mathematics is heavily dependent on understanding the exact meaning of its terms.
The Professor's pedagogical prescription:
1. Every elementary school should have access to a mathematics specialist. This person's purpose is to teach the teachers how to present mathematics with a modicum of skill and knowledge and a minimum of fear. Since most elementary school teachers (especially in the primary grades) are terrified of the subject, and, left to their own devices, would at least cheat on the time allotments, this specialist's mission is damage control.
2. Every secondary school should have at least two mathematics specialists on staff, one with a B.Sc. and the other with an M.Sc. in the subject. NOTE: "in the subject". A degree in education with a minor or concentration in teaching mathematics may be sufficient to understand and correctly teach high school mathematics curriculum up to grade ten, but not afterwards. A physics teacher might do, if one is available, and the chemistry mavens may manage. Others will merely take students by rote through individual book chapters, but do not know the subject well enough to integrate the material or impart understanding. Mathematics is intentionally learned through informed fingertips, not merely by rote.
Q. You're not one of these high-falutin' ivory-tower academics trying to re-establish the "new math" are you?
A1. My office is in the ivory basement.
A2. I taught high school myself for twelve years.
A3. I teach mathematics to prospective elementary school teachers.
A4. The "new math", like many well-intentioned educational experiments, was too ill-informed of conditions in the trenches to have any hope of success.
Q. How about some advice on specific issues while we wait for the miraculous advent of real mathematics teachers in the schools?
A. Glad to. What follows is a small collection of items I've noticed over the years in the category of get the language precise and accurate the first time. The list is by no means exhaustive of either this category or of mathematical pedagogy; it is merely illustrative.
Numerals are different from numbers
Numbers are mental ideas or abstractions that we employ for quantification. "How many popsicle sticks are there in the pile, Melissa?" Like all abstractions, they are not grasped until they have been successfully communicated. The latter is done by employing numerals, whether in spoken or written form. Thus, the idea of "fourness" is a number, but the symbols "four", "quatre", "IV", and "4" are numberals used to communicate the idea (number) from one person to another, hopefully triggering the same idea in the receiver's mind.
The primary teacher need not explain all this in detail, but it would take almost no effort to use the correct vocabulary, referring to what is written on the page as a "numeral". It's only one more syllable.
Zero is not nothing
One does not introduce the concept of zero right away in first grade. However it does come eventually, and when it does, one must not say that "zero is nothing" because it isn't. Rather, it is a number (and when written or spoken a numeral) to represent having no things (a very different concept). Students need a good grasp of zero to handle subtraction and place value, and later to understand exponents.
Subtraction is the inverse of addition
8 - 5 = 3
because
3 + 5 = 8
That is, subtraction is not so much an operation on its own as it is a way of undoing a particular addition. Note that the related sentences read in reverse order. Don't change this order.
Get multiplication right
3 times 5
means
3 groups of 5
The multiplier (first number) is the number of groups and the multiplicand is the number of items in each group. (The result is called the product--teach the vocabulary; it won't kill anybody.) Yes, I know you get the same answer the other way around, but it is a different question, and students need some convincing that switching the order produces the same result. (After all, it does not for subtraction.)
Teach multiplication tables
Some things are worth memorizing. The old way is best here. Students need an instinctive level of knowledge here--addition and multiplication facts so well memorized from constant repetition that their answers are instantaneous.
Division is the inverse of multiplication
15 divided by 5 = 3
because
3 times 5 = 15 Remember: 3 is the number of groups.
That is, division is not so much an operation on its own as it is a way of undoing a particular multiplication. Note that the related sentences read in reverse order. Don't change this order. Observe carefully what this division means. Start with 15 (dividend) items and put them into groups of 5 (divisor). How many groups are there? Ans: 3 (quotient). Many textbooks reverse this order and suppose that the divisor is the number of groups, which is inconsistent.
Dividing a non-zero number by zero is undefined (can't be done)
By the above, if
15 divided by 0 equalled, say n
then
n times 0 would equal 15
But, n groups of zero is zero, so this is impossible. Thus, there is no such number, or to put it another way, the result is undefined. So, you cannot divide by zero.
See what a little care got us? A simple explaination of something some people find hard to understand.
On the other hand,
zero divided by any number except zero is zero
Just reverse it to get the related multiplication, and this is obvious. So, every number is a factor of zero, and in particular, this means 0 is even.
On the gripping hand,
What is zero divided by itself?
Well, 0 divided by 0 would be some number, say n, provided n times zero is zero (per the above). But this is always true, regardless of the value of n. Hence, if follows that zero divided by zero can be anything you like. (We say the answer is indeterminate.)
Don't overdo calculator use
Calculators are useful, but if students cannot do basic arithmetic without them, they can't do more complicated arithmetic with them. Teach to understanding, not to button pushing.
Use the law of Proportions
An equality of two fractions is called a proportion.
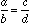
The four parts of a proportion are called terms. a, the first, and d the last, are the extremes. b, the second, and c, the third, are called the means.
By using equivalent fractions, one can easily see that this equality is true if and only if
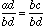
and since the denominators are equal this is the case if and only if the numerators are equal (you did do some work on equivalent fractions, didn't you?), that is, if and only if ad = bc.
Aha! sez you, that's called cross-multiplying. Please don't use this language!! Instead, say: In a proportion, the product of the extremes equals the product of the means. (The law of Proportions.) Never call it anything else, never (wash your mouth out with soap) call it cross multiplying, and be sure to apply this technique only where there is a proportion. (What goes wrong here is that students use "cross multiplication" every time they see two fractions--they have no contextual clues, so why not? If you call it the law of proportions and are careful to be consistent, they have a better chance of remembering the correct context in which to do this.)
Call a bracket a bracket
(these are parentheses)
[these are brackets]
{these are braces}
<these are angle brackets>
So when you teach order of operations, use the acronym PODMAS or PEODMAS
Parentheses
Exponents
Of
Division
Multiplication
Addition
Subtraction
Algebra is hopeless if students don't know the correct order of operations.
Logarithm is another name for exponent
'Nuff said? Demystify. Show your students that exponent, logarithm, and radical notations are all the same, just focusing on (isolating) a different one of the three numbers.
Define prime numbers correctly
The classic definition provided by Social Studies teachers to grade eight math classes, and which every first year university student can recite is "A prime is a number that is divisible by itself and one." This is, of course, wrong, for it allows the number one to be prime, which it is not, and is ambiguous about negative numbers. Rather, say:
A prime is a positive integer with exactly two factors.
Note that one is neither prime nor composite, and that zero (if you use it) is composite.
Define powers correctly
The classic definition of 25 provided by typical Social Studies teachers to grade eight math classes, and which every first year university student can recite is: "Two to the fifth means two multiplied by itself five times." No it doesn't! It means:
2 times 2 times 2 times 2 times 2
which has only four multiplications, not five as the pseudo-definition claims. There are five 2's (i.e. factors), not five multiplications. Say rather:
an means a number with n factors of a.
Spell correctly
Not long ago I picked from a bookstore shelf a popular work purporting to offer financial advice, in which, for every topic relating to investment, the amount of money at interest was called either the "principle" or the "capitol". Yikes! That's principal and capital, respectively. See our page on homophones for hundreds more examples.
The bottom line
Getting a job in any fourth civilization sector today (not a McJob) requires a technical education. This means obtaining as much mathematics skill as possible (at least to calculus). But calculus is heavily dependent on high school algebra, and students have no hope of understanding algebra if they are confused about arithmetic or have been told by their grade one teacher (body language is sufficient) either that mathematics is hard, or distasteful, or only for boys. Teach it right the first time, and you'll break the cycle of fear and ignorance. As in theology (there can only be one God) so in mathematics. It's not a matter of opinion; the answer is not whatever you feel like; precision of language matters; ideas are important; there is a right way. Find it out and follow it. Students need analytical techniques that lead to and follow from (feedback) general understanding. Memorization has its uses for getting started but eventually collapses of its own weight. (This is also true in language arts--you had better be teaching phonics!) Students either learn to abstract (generalize beyond the syntactical to semantic knowledge), or they cease to learn.
Like what you see? Want to exchange links? Want to contribute original or attributed material? Contact Us. If We use your material, We'll acknowledge the source.
|