A CONTRIBUTION TO THE MATHEMATICAL THEORY OF
BIG GAME HUNTING
H. PÉTARD, Princeton, New Jersey
This little known mathematical discipline has not, of recent years,
received in the literature the attention which, in our opinion, it
deserves. In the present paper we present some algorithms which, it is
hoped, may be of interest to other workers in the field. Neglecting the
more obviously trivial methods, we shall confine our attention to those
which involve significant applications of ideas familiar to
mathematicians and physicists.
The present time is particularly fitting for the preparation of an
account of the subject, since recent advances both in pure mathematics
and in theoretical physics have made available powerful tools whose
very existence was unsuspected by earlier investigators. At the same
time, some of the more elegant classical methods acquire new
significance in the light of modern discoveries. Like many other
branches of knowledge to which mathematical techniques have been
applied in recent years, the Mathematical Theory of Big Game Hunting
has a singularly happy unifying effect on the most diverse branches of
the exact sciences.
For the sake of simplicity of statement, we shall cofine our
attention to Lions (Felis leo) whose habitat is the Sahara
Desert. The methods which we shall enumerate will easily be seen to be
applicable, with obvious formal modifications, to other carnivores and
to other portions of the globe. The paper is divided into three parts,
which draw their material respectively from mathematics, theoretical
physics, and experimental physics.
The author desires to acknowledge his indebtness to the Trivial
Club of St. John's College, Cambridge, England; to the M.I.T. chapter
of the Society for Useless Research, to the F. o. P., of Princeton
University; and to numerous individual contributors, known and unknown,
conscious and unconscious.
1. Mathematical methods
- THE HILBERT, OR AXIOMATIC,
METHOD. We place a locked cage at a given point of the desert.
We then introduce the following logical system.
AXIOM I. The class of lions in the Sahara
Desert is non-void.
AXIOM II. If there is a lion in the Sahara
Desert, there is a lion in the cage.
RULE OF PROCEDURE. If p is a
theorem, and "p implies q" is a
theorem, then q is a theorem.
THEOREM I. There is a lion in the cage.
- THE METHOD OF INVERSE GEOMETRY. We place a
spherical cage in the desert, enter it, and lock it. We perform an
inversion with respect to the cage. The lion is then in the interior of
the cage, and we are outside.
- THE METHOD OF PROJECTIVE GEOMETRY. Without
loss of generality, we may regard the Sahara Desert as a plane. Project
the plane into a line, and then project the line into an interior point
of the cage. The lion is projected into the same point.
- THE
BOLZANO-WEIERSTRASS METHOD.
Bisect the desert by a line running N-S. The lion is either in the E
portion or in the W portion; let us suppose him to be in the W portion.
Bisect the portion by a line running E-W. The lion is either in the N
portion or in the S portion; let us suppose him to be in the N portion.
We continue this process indefinitely, constructing a sufficiently
strong fence about the chosen portion at each step. The diameter of the
chosen portions approaches zero, so that the lion is ultimately
surrounded by a fence of arbitrarily small perimeter.
- THE "MENGENTHEORETISCH" METHOD. We
observe that the desert is a separable space. It therefore contains an
enumerable dense set of points, from which can be extracted a sequence
having the lion as limit. We then approach the lion stealthily along
this sequence, bearing with us suitable equipment.
- THE PEANO METHOD.
Construct, by standard methods, a continuous curve passing through
every point of the desert. It has been
remarked(1) that it
is possible to traverse such a curve in an arbitrarily short time. Armed
with a spear, we traverse the curve in a time shorter than in which a
lion can move his own length.
- A TOPOLOGICAL METHOD. We observe that a lion
has at least the connectivity of the torus. We transport the desert
into four-space. It is then
possible(2) to carry
out such a deformation that the lion can be returned to three-space in
a knotted condition. He is then helpless.
- THE CAUCHY, OR
FUNCTIONTHEORETICAL, METHOD. We consider an analytic lion-valued
function f(z). Let
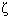 be
the cage. Consider the integral
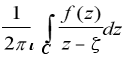
where C is the boundary of the desert; its value is
f(),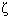
i.e., a lion in the cage(3).
- THE WIENER
TAUBERIAN METHOD. We procure a tame lion,
Lo,
of class L(-
 ,
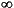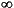), whose Fourier
transform nowhere vanishes, and release it in the desert.
Lo
then converges to our cage. By Wiener's General Tauberian
Theorem(4), any other lion,
L (say), will then converge to the same cage. Alternatively, we can
approximate arbitrarily closely to L by translating
Lo
about the desert(5).
2. Methods from theoretical physics
- THE DIRAC METHOD. We
observe that wild lions are, ipso facto, not observable in the Sahara
Desert. Consequently, if there are any lions in the Sahara, they are
tame. The capture of a tame lion may be left as an exercise for the
reader.
- THE SCHRÖDINGER
METHOD. At any given moment there is a positive probability that
there is a lion in the cage. Sit down and wait.
- THE METHOD OF NUCLEAR PHYSICS. Place a tame
lion in the cage, and apply a Majorana exchange
operator(6) between it
and a wild lion.
As a variant, let us suppose, to fix ideas, that we require a male
lion. We place a tame lioness in the cage, and apply a Heisenberg
exchange operator(7)
which exchanges the spins.
- A RELATIVISTIC METHOD. We distribute about
the desert lion bait containing large portions of the Companion of
Sirius. When enough bait has been taken, we project a beam of light
across the desert.This will bend right round the lion, who will then
become so dizzy that he can be approached with impunity.
3. Methods from experimental physics
- THE THERMODYNAMICAL METHOD. We construct a
semi-permeable membrane, permeable to everything except lions, and
sweep it across the desert.
- THE ATOM-SPLITTING METHOD. We irradiate the
desert with slow neutrons. The lion becomes radioactive, and a process
of disintegration sets in. When the decay has proceeded sufficiently
far, he will become incapable of showing fight.
- THE MAGNETO-OPTICAL METHOD. We plant a
large lenticular bed of catnip (Nepeta cataria), whose axis lies
along the direction of the horizontal component of the earth's magnetic
field, and place a cage at one of its foci. We distribute over the
desert large quantities of magnetized spinach (Spinacia
oleracea), which, as is well known, has a high ferric content. The
spinach is eaten by the herbivorous denizens of the desert, which are
in turn eaten by lions. The lions are then oriented parallel to the
earth's magnetic field, and the resulting beam of lions is focussed by
the catnip upon the cage.
- The American Mathematical Monthly, Aug.-Sept. 1938, pp.
446-447.
(1) By Hilbert. See E. W. Hobson, The
Theory of Functions of a Real Variable and the Theory of Fourier's
Series, 1927, vol. 1, pp. 456-457.
(2) H. Seifert and W. Threlfall,
Lehrbuch der Topologie, 1934, pp. 2-3.
(3) N.B. By Picard's Theorem
(W. F. Osgood, Lehrbuch der Funktionentheorie, vol. 1, 1928, p.748), we
can catch every lion with at most one exception.
(4) N. Wiener, l. c., p.
89.
(5) N. Wiener, The Fourier Integral
and Certain of its Applications, 1933, pp. 73-74.
(6) See, for example, H. A. Bethe and
R. F. Bacher, Reviews of Modern Physics, vol. 8, 1936, pp. 82-229;
especially pp. 106-107.
(7) Ibid.
At about the time Bourbaki was starting up, another group of wags
invented E. S. Pondiczery, a purported member of the Royal Institute of
Poldavia. The initials (E.S.P., R.I.P.) were inspired by a projected
but never written article on extra-sensory perception. Pondiczery's
main work was on mathematical curiosa. His proudest accomplishment was
the only known use of a second-degree pseudonym. Submitting a paper on
the mathematical theory of big-game hunting to The American
Mathematical Monthly, Pondiczery asked in a covering letter that he be
allowed to sign it with a pseudonym, because of the obviously facetious
nature of the material. The editor agreed, and the paper appeared (in
1938) under the name of H. Pétard.
- P. R. Halmos
Like what you see? Want to exchange links? Want to contribute original or attributed material? Contact Us. If We use your material, We'll acknowledge the source.
|
